NUMERICAL ABILITY
ACE ACADEMY IES ESE HANDWRITTEN CLASSROOM NOTES
ENGINEERING SERVICES GOVT JOBS EXAMINATION NOTES
FREE DOWNLOAD PDF
Numerical Ability Engineering Services IES ESE Ace Academy Notes PDF Free Download at CivilEnggForAll.com
PLEASE NOTE : MOST OF THE PDF’S AVAILABLE IN THE INTERNET WITH THE NAME OF IES ACE ACADEMY NOTES ARE FAKE. FOR THE SAKE OF INCREASING THEIR WEBSITE POPULARITY/TRAFFIC, FEW WEBSITES ARE ALLEGEDLY PROVIDING SOME USELESS MATERIALS WITH THE NAME OF IES ACE ACADEMY NOTES WHICH IN RETURN MIGHT RUIN STUDENT’S VALUABLE MARKS. TO HELP THE STUDENTS WHO ARE WORKING THEIR LEVEL BEST TO CRACK THE RANKS, WE ARE PROVIDING ONLY VERIFIED ACE ACADEMY IES NOTES HERE. BUT HOWEVER THERE MIGHT BE SOME MANUAL ERRORS IN THE CONTENT OF THIS BOOK.

Numerical Ability Engineering Services IES ESE Ace Academy Notes PDF
TOPICS COVERED IN THIS BOOK
- Boats and Streams
- Mixtures and Alligations
- Progressions
- Data Interpretation
- Clocks
- Blood Relations
- Indices and Surds
- Syllogism
- Directions
- Cubes and Dice
- Puzzles
- Number Systems
- Letter System
- Ratio and Proportions
- Problems on Age
- Percentages
- Profit and Loss
- Averages
- Time, Men and Work
- Pipes and Cisterns
- Time, Speed and Distance

TESTS OF DIVISIBILITY
- Divisibility By 2 : A number is divisible by 2, if its unit’s digit is any of 0, 2, 4, 6, 8 Ex. 84932 is divisible by 2 while 65935 is not.
- Divisibility By 8 : Anumber is divisible by 3, if the sum of its digits is divisible by 3 Ex. 592482 is divisible by 3, since sum of its digits (5+9+2+4+8+2) 30, which is divisible by 3 But, 864329 is not divisible by 3, since sum of its digits (8+6+4+3+2+9) 32, which is not divisible by 3
- Divisibility By 4 : A number is divisible by 4, if the number formed by the last two digits is divisible by 4. Ex. 892648 is divisible by 4, since the number formed by the last two digits is 48, which is divisible by 4 But, 749282 is not divisible by 4, since the number formed by the last two digits is 82, which is not divisible by 4
- Divisibility By 6 : A number is divisible by 5, if its unit’s digit is either o or 5 Thus, 20820 and 50345 are divisible by 5, while 30934 and 40946 are not.
- Divisibility By 6 : A number is divisible by 6, if it is divisible by both 2 and 3. Ex The number 35256 is elearly divisible by 2 Sum of its digits (3+5+2+5+6) 21, which is divisible by 3 Thus, 35256 is divisible by 2 as well as 3. Hence, 35256 is divisible by 6
- Divisibility by 8 : A number is divisible by 8 if the number formed by the last three digits of the given number is divisible by 8.
Ex : 953360 is divisible by 8, since the number formed by last three digits is 360, ehich is divisible by 8.
But, 529418 is not divisible by 8, since the number formed by last three digits is 418, which is not divisible by 8 - Divisibility By 9 : A number is divisible by 9, if the sum of its digits is divisible by 9 Ex. 60732 is divisible by 9, since sum of digits (6+0+7+3+2) 18, which is divisible by 9 But, 68956 is not divisible by 9, since sum of digits (6+8+9+6+6) 34, which is not divisible by 9
- Divisibility By 10 : A number is divisible by 10, if it ends with 0 Ex. 95410, 10480 are divisible by 10, while 96375 is not
- Divisibility By 11 : A number is divisible by 11, if the difference of the sum of its digits at odd places and the sum of its digits at even places, is either 0 or a number divisible by 11 Ex. The number 4832718 is divisible by 11, since (sum of digits at odd places) (sum of digits at even places) (8+7+3+4)-(1+2+8)=11, which is divisible by 11.
- Divisibility By 12 : A number is divisible by 12, if it is divisible by both 4 and Ex. consider the number 34632 (i) The number formed by last two digits is 32, which is divisible by 4 (ii) Sum of digits (3+4+6+3+2)=18, which is divisible by 3 Thus, 34632 is divisible by 4 as well as 3. Hence, 34632 is divisible by 12
- Divisibility By 14 : A number is divisible by 14, if it is divisible by 2 as well as 7
- Divisibility By 15 : A number is divisible by 15, if it is divisible by both 3 and itself
- Divisibility By 16 : A number is divisible by 16, if the number formed by the last digits is divisible by 16 Ex. 7957536 is divisible by 16, since the number formed by the last four digits is 7536, which is divisible by 16
- Divisibility By 24 : A given number is divisible by 24, if it is divisible by both 3 and 8
- Divisibility By 40 : A given number is divisible by 40, if it is divisible by both 5 and 8
- Divisibility By 80 : A given number is divisible by 80, if it is divisible by both 5 and 16 Note If a number is divisible by p as well as q, where p and g are co-primes, then the given number is divisible by pq If p and g are not co-primes, then the given number need not be divisible by pa, even when it is divisible by both p and g Ext. 36 is divisible by both 4 and 6, but it is not divisible by (4 x 6) 24, since 4 and 6 are not co-primes

PROGRESSION :
A succession of numbers formed and arranged in a definite order according to certain definite rule is called a progression.
- Arithmetic Progression (A.P): If each term of a progression differs from its preceding constant, such a progression is called an arithmetical progression. This constant difference is called the common difference of the A.P An A.P with first term a and common difference d is given by a, (a+d), (a+2d), (a+3d),…
The nth term of this AP is given by Tn = a(n-1)d.
The sum of n terms of this A.P Sn = n(First term+Last Term)/2 - Geometrical Progression (G.P): A progression of numbers in which every term bears a constant ratio with its preceding term, is called a geometrical progression The constant ratio is called the common ratio of the G.P
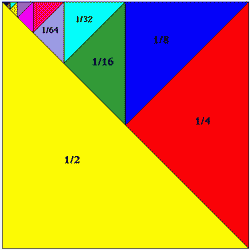
A G.P with first term a and common ratio r is a, ar, ar² ar³,…
T(n) = ar^(n-1)
DOWNLOAD LINK : Numerical Aptitude Engineering Services IES ESE Ace Academy Handwritten Classroom Notes Free Download PDF
PASSWORD : CivilEnggForAll
OTHER USEFUL LINKS FROM CIVILENGGFORALL
ENVIRONMENTAL ENGINEERING ENGINEERING SERVICES IES ESE EXAM ACE NOTES : CLICK HERE
GEOTECHNICAL ENGINEERING ENGINEERING SERVICES IES ESE EXAM ACE NOTES : CLICK HERE
RCC ACE ACADEMY IES EXAM HANDWRITTEN NOTES : CLICK HERE
STRENGTH OF MATERIALS ACE ACADEMY IES EXAM NOTES : CLICK HERE
TRANSPORTATION ENGINEERING ACE ACADEMY IES EXAM NOTES : CLICK HERE
HYDROLOGY ACE ACADEMY IES EXAM NOTES : CLICK HERE
IRRIGATION ACE ACADEMY IES EXAM NOTES : CLICK HERE
SURVEYING ACE ACADEMY IES EXAM NOTES : CLICK HERE
MATHS MADE EASY HANDWRITTEN NOTES : CLICK HERE
REASONING AND APTITUDE MADE EASY GATE HANDWRITTEN NOTES : CLICK HERE
OPEN CHANNEL FLOW MADE EASY GATE HANDWRITTEN NOTES : CLICK HERE
ENGINEERING MECHANICS MADE EASY GATE HANDWRITTEN NOTES : CLICK HERE





















