CALCULUS ENGINEERING MATHEMATICS GATE 2020 STUDY MATERIAL PDF CIVILENGGFORALL

Functions of Single Variable Limits
L’ Hospital’s Rule
Continuity and Discontinuity
Differentiability
Mean Value Theorems
Functions of Two Variables
Computing the Derivative
Partial Derivatives
Maxima and Minima of Functions of Two Variables
Taylor and Maclaurin Series
Some Standard Integrations
Definite Integral
Multiple Integrals
Change of Order of Integration
Applications of the Definite Integral
Volume: Slicing and Disks
Vector
Product of Two Vectors
Vector Calculus
Directional Derivative
Divergence
Curl
Line Integral
Surfaces
Volume Integral
Stoke’s Theorem
Green Theorem
Gauss’s Divergence Theorem

MAXIMA AND MINIMA OF FUNCTIONS OF TWO VARIABLES

A function f(x, y) is said to have a maximum or minimum at x = a, y = b, according as f(a + h, b + k) is less or greater than f(a, b) for all positive or negative small values of h and k.

In other words, if Δ = f(a + h, b + k) – f(a, b) is of the same sign for all small values of h, k and if this sign is negative, then f(a, b) is a maximum. If this sign is positive, then f(a, b) is a minimum. A maximum or minimum value of a function is called its extreme value.

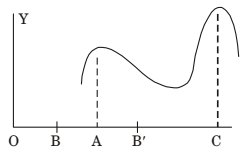
Above figure shows a graph of the function f(x) and OA = a, i.e., f(x) has a maximum value for x = a because f(a) has a value more than the values of f(x) for every value of x between B and B’. f(x) is said to be a maximum at x = a, even though value of f(x) at x = a should be greater than all other values of f(x) in some small neighbourhood. Thus a maximum value of f(x) is not necessarily the greatest value of f(x). In fact, a curve might have several maxima (and minima).

GATE 2020 STUDY MATERIALS FOR CIVIL ENGINEERING : CLICK HERE

ACE ACADEMY GATE STUDY MATERIALS FOR CIVIL ENGINEERING : CLICK HERE

MADE EASY GATE NOTES FOR CIVIL ENGINEERING : CLICK HERE

Finding Absolute Maxima and Minima Values Working Rules:

If f is a differentiable function in [a b] except at finitely many points, then to find absolute maximum and absolute minimum values, adopt following procedure: (i) Evaluate f(x) at the points, where f’(x) = 0. (ii) Evaluate f(a) and f(b).

Then maximum of these values is the absolute maxima and minimum of these values is called absolute minima.

MULTIPLE INTEGRALS

Let a single-valued and bounded function f(x,y) of two independent variables x,y be defined in a closed region R of the xy-plane. Divide the region R into sub-regions by drawing lines parallel to co-ordinate axes. Number the rectangles which lie entirely inside the region R from 1 to n.

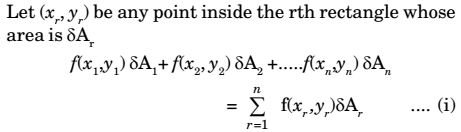
Let number of these sub-regions increases indefinitely such that the largest linear dimension (i.e. diagonal) of δA_r approaches zero. The limit of the sum(i), if it exists, irrespective of the mode of sub-division, is called double integral of f(x,y) over the region R and is denoted by ʃʃ_Rf(x,y)dA

VECTOR : Vector is completely specified by its magnitude and direction. Vector is represented by a directed line segment. Thus PQ represents a vector where magnitude is the length PQ and direction is form P (starting point) to Q (end point)

Unit Vector : A vector of unit magnitude is called unit vector. Unit vector corresponding to vector A is written as A with a bar on it.

Null Vector : A vector of zero magnitude, which can have no direction associated with it is called zero (or null) vector and is denoted by O-a thick zero.