HYDRAULICS STUDY MATERIAL FOR SSC JE BY CIVILENGGFORALL FREE DOWNLOAD PDF

Hydraulics
Kinematics of Flow
Continuity Equations
Fluid Displacements
Circulation
Stream Function
Correction Factors
Turbulent Flow
Boundary Layer Theory
Open Channel Flow
Pumps And Turbines
Specific Speed
Turbines
Cavitation
Dimensional Analysis
Ship Model Testing

Fluid Pressure

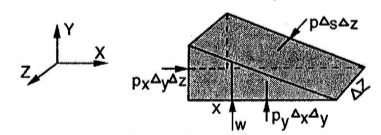
It is the pressure transmitted with equal intensity in all directions and acts normal to any plane. It is defined by limiting equation,

Pressure at a Point (Pascal’s Law)

Pressure intensity at a point is defined as the ratio of force acting on an elemental area and the elemental area as the area tends to zero at the point. This pressure is always normal to the surface, as fluid at rest cannot sustain any shear stress. If an elemental area is allowed to rotate freely in a fluid at rest, the pressure on the area will be of constant magnitude and is independent of the orientation of the area at the point. Then the pressure being scalar quantity must be same in all directions at a point. This is known as Pascal’s Law. Pressure at a point can be considered at the average of any three mutually perpendicular normal compressive stresses at a point, i.e. 1/3 (p_x + p_y + p_z)

HYDRAULIC MACHINERY IES MASTER GATE STUDY MATERIAL PDF: CLICK HERE

Newtonian Fluids

Newtonian fluids tend to have a certain constant viscosity. For instance, many common fluids air, water, light oils gasoline or shear stress is linearly dependent upon velocity gradient.

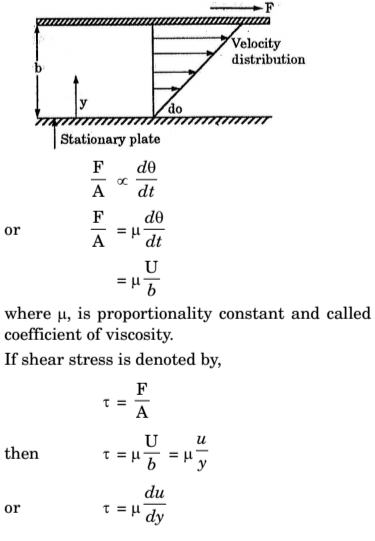
The rate change of angular deformation is proportional to the shear stress, i.e.

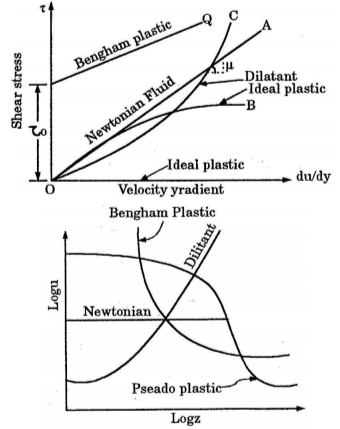
Shear Stress vs Velocity Gradient, Logu vs Logz

A Newtonain fluid is a special case of power law fluid having n = 1 and B = 0 and the constant A varying only with the type of fluid.

Ideal Fluid

It has been utilised in the analytical treatment of flow phenomenon. An imaginary flow of fluid non viscous and incompressible (inelastic) is known as ideal fluid. In ideal fluid shear stress is linearly dependent on velocity gradient.

Buoyancy and Floatation

Archimedes Principle

When a body is totally or partially immersed in a fluid, it is lifted up by a force which is equal to the weight of the fluid displaced by the body. This vertical upward force is called the center of buoyancy (C.B) and it is at the center of gravity of the displaced fluid.

Stability of Submerged Bodies

For stability of submerged body, the center of gravity of the body must lie directly below the center of buoyancy (gravity) of the displaced fluid. The submerged body is in neutral equilibrium of all positions as long as the w.f. of the body and C.B. coincides.

FLUID MECHANICS ACE GATE STUDY MATERIAL PDF: CLICK HERE

Floatation

A body immersed in any fluid is acted upon by weight of body W acting vertically downward and buoyant force Fb acting vertically upwards. If W > F_B, the body will sink. If W = F_B, the body will remain in equilibrium at any level. If W < F_B, the buoyant force will move the body upwards and the body will come to rest, when the buoyant force becomes equal to its weight. Then the body is said to be floating.

Principal of Floatation

The weight of a floating body is equal to the weight of the fluid displaced by the body.

Stability of Floating Bodies

For stability of floating cylinder or spheres the center of buoyancy (C.B.) should lie considerably below the w.f. (G) the body. Stability of other floating bodies will depend upon whether a righting or overturning moment is developed when the w.f. and C.B. move out of the vertical alignment due to the shifting of the position of C.B. The C.B. will shift because of the floating body tilts, the shape of displaced liquid changes and hence its w.f. shifts.

KINEMATICS OF FLOW

A particular quantity of matter or specified region in space is designated as a ‘System’. All matter external to system is called its ‘Surroundings’. A closed system refers to a specified mass limited by the boundaries, e.g. a kg mass of air contained in a cylinder.
An open system or control volume refers to definite fixed region in space through which the matter moves e.g., flow of air through a pipe.
Process is a path of succession of state through which the systems passes e.g., change in pressure, velocity, elevation, density, temperature.

FLUID MECHANICS ACE ACADEMY GATE NOTES PDF: CLICK HERE

FLUID DISPLACEMENTS

Consider all possible motion of a cubical fluid element.

(a) Translations: When this element is bodily moved from one position to another position, such that the median lines do not change in length and they are parallel to their respective former positions, then the movement is called translation.

(b) Linear Deformation: When there is change in the length of median line without change in the orientation, such a type of motion is called linear deformation. Two dimensional fluid element of constant density will have both side lengths altered due to linear deformation.

Fluid Displacements – Translation and Linear Deformation

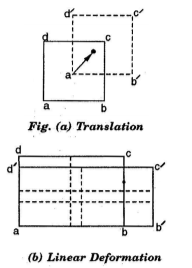
(c) Angular Deformation: When the angle between two adjacent sides of a fluid element change such a type of motion is called angular deformation. The angular deformation results in an incompressible fluid, the volume of the fluid element remains constant, while the deformation takes place.

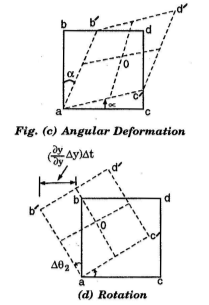
Fluid Displacements – Angular Deformation and Rotation

(d) Rotation: In the Fig. (d), the fluid element bodily rotates about the z-axis, i.e. perpendicular to the paper at point a. The average of the sum of the angular velocities of sides ab and ad is the net rotation of the fluid element about z-axis.

BOUNDARY LAYER THEORY

Prandtl gave a hypothesis, the fluid flowing along a solid wall may be divided into two independent regions:

Fluid within a thin region adjacent to the boundary where the viscous effects are predominant and in know as boundary layer.
Fluid outside this region, where ideal fluid flow exits. This region is known as main flow and velocity in this region approaches the free stream or potential velocity U.

Boundary Layer Flow over a Flat Plate

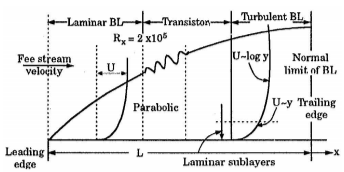
Consider a flat plate at zero incidence in an infinite extent of fluid. The fluid approaches the plate with uniform velocity U (or free stream velocity). As soon as it touches the plate at its leading edge, its velocity reduces to zero in accordance with the no slip condition. The velocity changes rapidly from zero at the boundary to its full value U within a short distance normal to the plate causing a large velocity gradient to developed in the boundary layer. Therefore even for a less viscous fluid (e.g. air or water) large shear resistance is developed over the plate and there by a sufficiently thick boundary layer is formed along the plate. As the flow proceeds downstream more fluid is retarded in the lateral direction thereby cursing boundary layer growth in the direction of flow.

Boundary Layer Thickness

Velocity of fluid u becomes zero at the stationary wall and becomes equal to free stream velocity U at certain distance normal to the plate. This variation becomes asymptotic in the vertical direction and hence this distance required will be too large to acquire free stream velocity U.