PERMUTATIONS AND COMBINATIONS, PROBABILITY GATE 2020 STUDY MATERIAL PDF CIVILENGGFORALL

PERMUTATIONS AND COMBINATIONS
PROBABILITY
Exercises, Problems, Solutions and hints on the above topics

PERMUTATIONS AND COMBINATION PERMUTATIONS

Each of the arrangements which can be made by taking some or all of a number of items is called a Permutation. Permutation implies “arrangement” or that “order of the items” is important. Permutations of three items a, b and c taken two at a time are ab, ba, ac, ca, cb and bc. Since the order in which items are taken is important, ab and ba are counted as two different permutations. The words “permutation” and “arrangement” are synonymous and can be used interchangeably.” Number of permutations of n things taking r at a time is denoted by ⁿP_r (and read as “nPr”)

COMBINATIONS

Each of the groups or selections which can be made by taking some or all of a number of items is called Combination. I n combinations, order in which the items are taken is not considered as long as the specific things are included. Combinations of three items a, b and c taken two at a time are ab, bc and ca. Here, ab and ba are not considered separately because the order in which a and b are taken is not important but it is only required that a combination including a and b is what is to be counted. Words “combination” and “selection” are synonymous. Number of combinations of n things taking r at a time is denoted by ⁿC_r (and read as “nCr”)

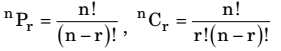
Number of ways in which n things may be arranged taking them all at a time, when p of the things are exactly alike of one kind, q of them exactly alike of another kind, r of them exactly alike of a third kind, and the rest all distinct is n!/p!q!r!
Number of ways of selecting one or more items from n given items = 2ⁿ – 1
Number of ways of dividing (p + q) items into two groups of p and q items respectively is (p+q)!/p!q!
Number of ways of dividing 2p items into two equal groups of p each is (2p)!/(p!)² where two groups have distinct identity.

Number of ways of dividing 2p items into two equal groups of p each is (2p)!/2!(p!)² where two groups do not have distinct identity.
Number of ways in which (p + q + r) things can be divided into three groups containing p, q and r things respectively is (p+q+r)!/p!q!r!
Number of circular arrangements of n distinct items is (n – 1)! If there is a difference between clockwise and anticlockwise arrangements and (n – 1)!/2 if there is no difference between clock wise and anticlockwise arrangements.