FLUID MECHANICS TEXTBOOK BY CIVILENGGFORALL FREE DOWNLOAD PDF

TOPICS COVERED

INTRODUCTION TO FLUID MECHANICS
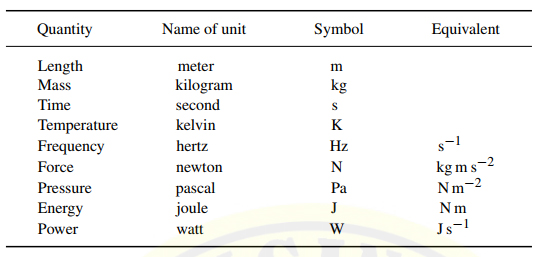
UNITS OF MEASUREMENT
SOLIDS, LIQUIDS AND GASES
CONTINUUM HYPOTHESIS’
SURFACE TENSION
FLUID STATICS
CLASSIC THERMODYNAMICS
PERFECT GAS
STATIC EQUILIBRIUM OF A COMPRESSIBLE MEDIUM
CARTESIAN TENSORS
SCALARS AND VECTORS
ROTATION OF AXES
MULTIPLICATION OF MATRICES
SECOND-ORDER TENSOR
CONTRACTION AND MULTIPLICATION
FORCE ON A SURFACE
KRONECKER DELTA AND ALTERNATING TENSOR
DOT PRODUCT
CROSS PRODUCT
OPERATOR V : GRADIENT, DIVERGENCE AND CURL
SYMMETRIC AND ANTISYMMETRIC TENSORS
EIGENVALUES AND EIGENVECTORS OF A SYMMETRIC TENSOR
GAUSS THEOREM
STOKES THEOREM
COMMA NOTATION
BOLDFACE VS INDICIAL NOTATION
INTRODUCTION TO KINEMATICS
LAGRANGIAN AND EULERIAN SPECIFICATIONS
EULERIAN AND LAGRANGIAN DESCRIPTION
STREAMLINE, PATHLINE AND STREAKLINE
REFERENCE FRAME AND STREAMLINE PATTERN
LINEAR STRAIN RATE
SHEAR STRAIN RATE
VORTICITY AND CIRCULATION
RELATIVE MOTION NEAR A POINT
KINEMATIC CONSIDERATION OF PARALLEL SHEAR FLOWS
KINEMATIC CONSIDERATION OF VORTEX FLOWS
ONE, TWO, THREE DIMENSIONAL FLOWS
THE STREAMFUNCTION
POLAR COORDINATES

INTRODUCTION TO CONSERVATION LAWS
TIME DERIVATIVES OF VOLUME INTEGRALS
CONSERVATION OF MASS
GENERALIZED AND REVISITED STREAMFUNCTIONS
ORIGIN OF FORCES IN FLUID
STRESS AT A POINT
CONSERVATION OF MOMENTUM
MOMENTUM PRINCIPLE FOR A FIXED VOLUME
ANGULAR MOMENTUM PRINCIPLE FOR A FIXED VOLUME
CONSTITUTIVE EQUATION FOR NEWTONIAN FLUID
NAVIER-STOKES EQUATION
ROTATING FRAME
MECHANICAL ENERGY EQUATION
FIRST LAW OF THERMODYNAMICS
SECOND LAW OF THERMODYNAMICS
BERNOULLI EQUATION
APPLICATIONS OF BERNOULLI’S EQUATION
BOUSSINESQ APPROXIMATION
BOUNDARY CONDITIONS
INTRODUCTION TO VORTICITY DYNAMICS
VORTEX LINES AND VORTEX TUBES
ROLE OF VISCOSITY IN ROTATIONAL AND IRROTATIONAL VORTICES
KELVIN’S CIRCULATION THEOREM
VORTICITY EQUATION IN A NONROTATING FRAME
VELOCITY INDUCED BY A VORTEX FILAMENT
VORTICITY EQUATION IN A ROTATING FRAME
INTERACTION OF VORTICES
VORTEX SHEET
IRROTATIONAL FLOW
RELEVANCE OF IRROTATIONAL FLOW THEORY
VELOCITY POTENTIAL
LAPLACE EQUATION
APPLICATION OF COMPLEX VARIABLES
FLOW AT A WALL ANGLE
SOURCES AND SINKS
IRROTATIONAL VORTEX
DOUBLET
FLOW PAST A HALF BODY
FLOW PAST A CIRCULAR CYLINDER WITHOUT AND WITH CIRCULATION
FORCES ON A TWO DIMENSIONAL BODY
CONFORMAL MAPPING

GRAVITY WAVES
WAVE EQUATION
INFLUENCE OF SURFACE TENSION
SURFACE GRAVITY WAVES
HYDRAULIC JUMP
STOKES DRIFT
DYNAMIC SIMILARITY
BUCKINGHAM’S PIE THEOREM
LAMINAR FLOW
STEADY FLOW IN A PIPE
PRESSURE CHANGES
IMPULSIVELY STARTED PLATE
DIFFUSION OF VORTEX SHEET
CREEPING FLOW AROUND A SPHERE
BOUNDARY LAYERS AND RELATED TOPICS
BOUNDARY LAYER APPROXIMATION
SEPARATION
TWO DIMENSIONAL JETS
EFFECT OF PRESSURE GRADIENT
PERTURBATION TECHNIQUES
COMPUTATIONAL FLUID DYNAMICS
INSTABILITY
TURBULENCE
GEOPHYSICAL FLUID DYNAMICS
WAVES AND INSTABILITY
AERODYNAMICS AND RELATED CONCEPTS
COMPRESSIBLE FLOW
SONIC PROPERTIES
MACH CONE
BIOFLUID MECHANICS

Fluid Mechanics

Fluid mechanics deals with the flow of fluids. Its study is important to physicists, whose main interest is in understanding phenomena. They may, for example, be interested in learning what causes the various types of wave phenomena in the atmosphere and in the ocean, why a layer of fluid heated from below breaks up into cellular patterns, why a tennis ball hit with “top spin” dips rather sharply, how fish swim, and how birds fly.

FLUID MECHANICS ACE GATE STUDY MATERIAL : CLICK HERE

The study of fluid mechanics is just as important to engineers, whose main interest is in the applications of fluid mechanics to solve industrial problems. Aerospace engineers may be interested in designing airplanes that have low resistance and, at the same time, high “lift” force to support the weight of the plane. Civil engineers may be interested in designing irrigation canals, dams, and water supply systems. Pollution control engineers may be interested in saving our planet from the constant dumping of industrial sewage into the atmosphere and the ocean. Mechanical engineers may be interested in designing turbines, heat exchangers, and fluid couplings. Chemical engineers may be interested in designing efficient devices to mix industrial chemicals.

The objectives of physicists and engineers, however, are not quite separable because the engineers need to understand and the physicists need to be motivated through applications. Fluid mechanics, like the study of any other branch of science, needs mathematical analyses as well as experimentation. The analytical approaches help in finding the solutions to certain idealized and simplified problems, and in understanding the unity behind apparently dissimilar phenomena. Needless to say, drastic simplifications are frequently necessary because of the complexity of real phenomena. A good understanding of mathematical techniques is definitely helpful here, although it is probably fair to say that some of the greatest theoretical contributions have come from the people who depended rather strongly on their unusual physical intuition, some sort of a “vision” by which they were able to distinguish between what is relevant and what is not.

FLUID MECHANICS MADE EASY GATE NOTES : CLICK HERE

Kinematics

Kinematics is the branch of mechanics that deals with quantities involving space and time only. It treats variables such as displacement, velocity, acceleration, deformation, and rotation of fluid elements without referring to the forces responsible for such a motion. Kinematics therefore essentially describes the “appearance” of a motion. The forces are considered when one deals with the dynamics of the motion.

FLUID MECHANICS IES MASTER GATE STUDY MATERIAL : CLICK HERE

One, Two and Three Dimensional Flows

A truly one-dimensional flow is one in which all flow characteristics vary in one direction only. Few real flows are strictly one dimensional. Consider the flow in a conduit. The flow characteristics here vary both along the direction of flow and over the cross section. However, for some purposes, the analysis can be simplified by assuming that the flow variables are uniform over the cross section. Such a simplification is called a one-dimensional approximation, and is satisfactory if one is interested in the overall effects at a cross section. A two-dimensional or plane flow is one in which the variation of flow characteristics occurs in two Cartesian directions only.

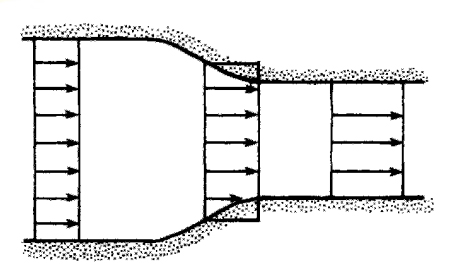
The flow past a cylinder of arbitrary cross section and infinite length is an example of plane flow. Note that in this context the word “cylinder” is used for describing any body whose shape is invariant along the length of the body. It can have an arbitrary cross section. A cylinder with a circular cross section is a special case. Sometimes, however, the word “cylinder” is used to describe circular cylinders only. Around bodies of revolution, the flow variables are identical in planes containing the axis of the body. Using cylindrical polar coordinates (R, ϕ, x), with x along the axis of the body, only two coordinates (R and x) are necessary to describe motion. The flow could therefore be called “two dimensional” (although not plane), but it is customary to describe such motions as three-dimensional axisymmetric flows

FLUID MECHANICS TEXTBOOK BY CIVILENGGFORALL

DOWNLOAD LINK : CLICK HERE

PASSWORD : CivilEnggForAll