STRENGTH OF MATERIALS AND STRUCTURES TEXTBOOK BY CIVILENGGFORALL FREE DOWNLOAD PDF

TOPICS COVERED

Introduction to Strength of Materials
Tension and Compression (Direct stresses)
Pin-jointed Frames or Trusses
Shearing Stress
Joints and Connections
Analysis of Stress and Strain
Thin Shells under Internal Pressure
Bending Moments and Shearing Forces
Geometrical properties of cross-sections
Longitudinal Stresses in beams
Shearing stresses in beams
Beams of two materials
Bending stresses and direct stresses combined
Deflection of Beams
Built-in and continuous beams
Plastic bending of mild-steel beams
Torsion of circular shafts and thin-walled tubes
Energy methods
Buckling of columns and beams
Lateral deflections of circular plates
Torsion of non-circular sections
Thick circular cylinders, discs and spheres
Introduction to matrix algebra
Matrix methods of structural analysis
The finite element method
Structural vibrations

STRENGTH OF MATERIALS – INTRODUCTION

The strength of a material, whatever its nature, is defined largely by the internal stresses, or intensities of force, in the material. A knowledge of these stresses is essential to the safe design of a machine, aircraft, or any type of structure. Most practical structures consist of complex arrangements of many component members; an aircraft fuselage, for example, usually consists of an elaborate system of interconnected sheeting, longitudinal stringers, and transverse rings. The detailed stress analysis of such a structure is a difficult task, even when the loading conditions are simple. The problem is complicated further because the loads experienced by a structure are variable and sometimes unpredictable. We shall be concerned mainly with stresses in materials under relatively simple loading conditions

IES MASTER STRENGTH OF MATERIALS GATE MATERIAL : CLICK HERE

STRETCHING OF A STEEL WIRE

One of the simplest loading conditions of a material is that of tension, in which the fibres of the material are stretched. Consider, for example, a long steel wire held rigidly at its upper end, and loaded by a mass hung from the lower end. If vertical movements of the lower end are observed during loading it will be found that the wire is stretched by a small, but measurable, amount from its original unloaded length. The material of the wire is composed of a large number of small crystals which are only visible under a microscopic study; these crystals have irregularly shaped boundaries, and largely random orientations with respect to each other; as loads are applied to the wire, the crystal structure of the metal is distorted.

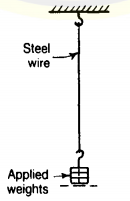
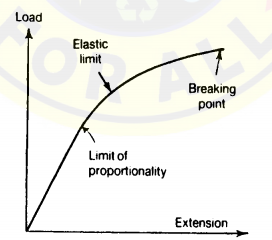
For small loads it is found that the extension of the wire is roughly proportional to the applied load. This linear relationship between load and extension was discovered by Robert Hooke in 1678; a material showing this characteristic is said to obey Hooke’s law. As the tensile load in the wire is increased, a stage is reached where the material ceases to show this linear characteristic; the corresponding point on the load-extension curve is known as the limit of proportionality. If the wire is made from a high-strength steel then the load-extension curve up to the breaking point has the form. Beyond the limit of proportionality the extension of the wire increases non-linearly up to the elastic limit and, eventually, the breaking point. The elastic limit is important because it divides the load-extension curve into two regions. For loads up to the elastic limit, the wire returns to its original unstretched length on removal of the loads; this property of a material to recover its original form on removal of the loads is known as elasticity; the steel wire behaves, in fact, as a still elastic spring. When loads are applied above the elastic limit, and are then removed, it is found that the wire recovers only part of its extension and is stretched permanently; in this condition the wire is said to have undergone an inelastic, or plastic, extension. For most materials, the limit of proportionality and the elastic limit are assumed to have the same value. In the case of elastic extensions, work performed in stretching the wire is stored as strain energy in the material; this energy is recovered when the loads are removed. During inelastic extensions, work is performed in making permanent changes in the internal structure of the material; not all the work performed during an inelastic extension is recoverable on removal of the loads; this energy reappears in other forms, mainly as heat. The load-extension curve is not typical of all materials; it is reasonably typical, however, of the behaviour of brittle materials. An important feature of most engineering materials is that they behave elastically up to the limit of proportionality, that is, all extensions are recoverable for loads up to this limit. The concepts of. linearity and elasticity t form the basis of the theory of small deformations in stressed materials.

STRENGTH OF MATERIALS ACE GATE MATERIAL : CLICK HERE

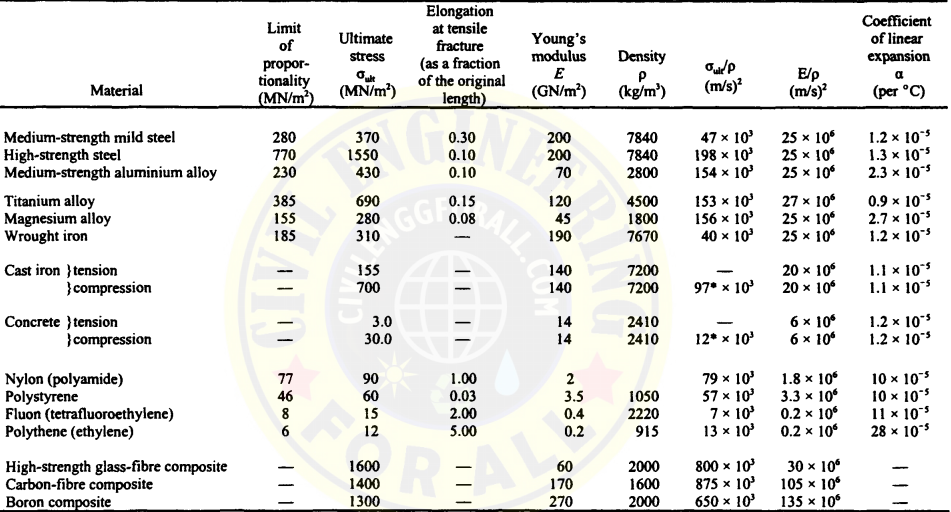
Load-extension curve for a steel wire, showing the limit of linear-elastic behaviour (or limit of proportionality) and the breaking point

Strength properties of some engineering materials

Most of the materials are in common engineering use, including a number of relatively new and important materials; namely glass-fibre composites, carbon-fibre composites and boron composites. In the case of some brittle materials, such as cast iron and concrete, the ultimate stress in tension is considerably smaller than in compression.

Strength properties of few engineering materials

STRENGTH OF MATERIALS MADE EASY GATE NOTES : CLICK HERE

Composite materials, such as glass fibre reinforced plastics, (GRP), carbon-fibre reinforced plastics (CFRP), boron-fibre reinforced plastics, ‘Kevlar’ and metal-matrix composites are likely to revolutionise the design and construction of many structures in the 21st century. The glass fibres used in GRP are usually made from a borosilicate glass, similar to the glass used for cooking utensils. Borosilicate glass fibres are usually produced in ‘E’ glass or glass that has good electrical resistance. A very strong form of borosilicate glass fibre appears in the form of ‘S’ glass which is much more expensive than ‘E’ glass. Some carbon fibres, namely high modulus (HM) carbon fibres, have a tensile modulus much larger than high strength steels, whereas other carbon fibres have a very high tensile strength (HS) much larger than high tensile steels. Currently ‘S’ glass is some eight times more expensive than ‘E’ glass and HS carbon is about 50 times more expensive than ‘E’ glass. HM carbon is some 250 times more expensive than ‘E’ glass while ‘Kevlar’ is some 15 times more expensive than ‘E’ glass.